Trong toán học, khái niệm mặt phẳng trung trực được dùng để chỉ một mặt phẳng vuông góc tại trung điểm của đường thẳng. Mặt phẳng này có nhiều tính chất quan trọng hỗ trợ người học dựng hình dễ dàng trong không gian. Bài viết sau đây sẽ trình bày chi tiết về mặt phẳng vuông góc này.
Định nghĩa mặt phẳng trung trực là gì?
Như đã nói, mặt phẳng trung trực là một mặt phẳng có phương vuông góc với một đường thẳng tại trung điểm của nó. Dưới đây là một vài ví dụ cụ thể để bạn hiểu rõ hơn về kiểu mặt phẳng này.
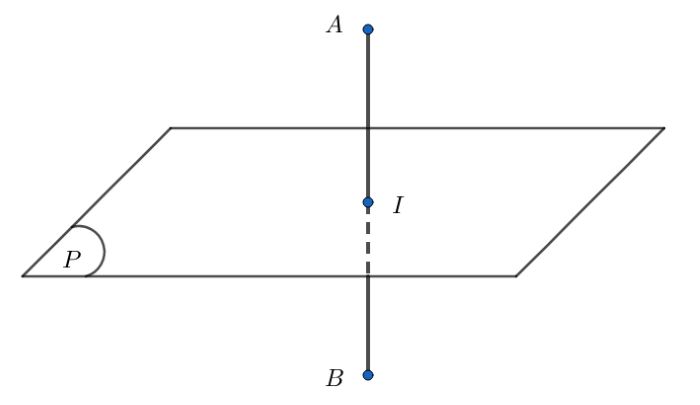
Theo như hình vẽ trên, đoạn thẳng AB có trung điểm I cách đều 2 đầu mút A và B của đoạn thẳng. Một mặt phẳng (P) cắt đoạn thẳng theo phương vuông góc tại trung điểm I. Do đó, người ta sẽ gọi (P) là mặt phẳng trung trực của đoạn thẳng AB tại điểm I.
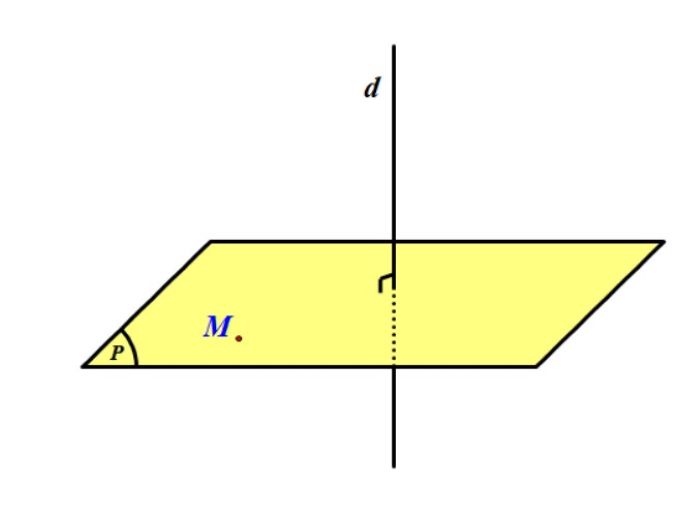
Ví dụ tiếp theo biểu thị mối quan hệ giữa mặt phẳng (P) và đường thẳng (d). Theo như hình vẽ, đường thẳng (d) sẽ cắt mặt phẳng (P) theo phương vuông góc. Tuy nhiên, đường thẳng có thể kéo dài vô hạn và không có trung điểm. Do đó, mặt (P) trong trường hợp này không được gọi là mặt phẳng trung trực dù có vuông góc với đường thẳng.
Tóm lại, để (P) trở thành mặt phẳng trung trực thì cần thỏa mãn được các điều kiện cần và đủ sau:
- Mặt phẳng phải vuông góc với đoạn thẳng.
- Mặt phẳng phải đi qua trung điểm của đoạn thẳng.
Như vậy, khái niệm này được dùng để chỉ mối tương quan giữa mặt phẳng và đoạn thẳng chứ không phải đường thẳng.
Các tính chất liên quan của mặt phẳng trung trực
Tính chất đầu tiên của mặt phẳng trung trực là mọi điểm nằm trên mặt phẳng đều cách đều hai đầu mút đoạn. Do mặt phẳng cắt đoạn thẳng tại trung điểm của đoạn thẳng.
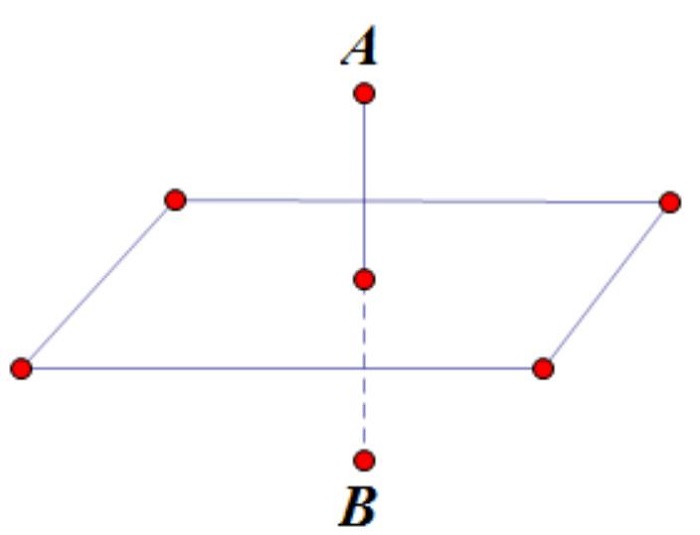
Khi một mặt phẳng (P) vuông góc với đường thẳng AB tại trung điểm I, thì đoạn thẳng MN hay đường thắng (d) song song với đường thẳng AB thì sẽ vuông góc với mặt phẳng (P). Ngược lại, nếu mặt phẳng (Q) song song với mặt phẳng (P) thì sẽ vuông góc với đường thẳng AB trong trường hợp này.
Với một đoạn thẳng, ta chỉ có thể dựng được một và chỉ một phẳng trung trực của đoạn thẳng đó. Theo đó, một đoạn thẳng AB cho trước có trung điểm là I thì sẽ có duy nhất một mặt phẳng (P) đi qua trung điểm đó và vuông góc với đoạn thẳng. Ngược lại, cũng có sẽ duy nhất một đoạn thẳng AB đi qua điểm I thuộc mặt phẳng (P) và vuông góc với mặt phẳng này.
Hướng dẫn cách vẽ mặt phẳng trung trực của đoạn thẳng
Để dựng được một mặt phẳng trung trực của đoạn thẳng, người học cần nắm rõ các tính chất song song, vuông góc có liên quan giữa mặt phẳng và đoạn thẳng. Trong hình học, mặt phẳng (P) sẽ được biểu hiện dưới dạng hình bình hành.
Theo đó, mặt phẳng (P) có một điểm cho trước là I. Người học chỉ cần vẽ thêm đoạn thẳng AB đi qua mặt phẳng và vuông góc với mặt phẳng sao cho độ dài của đoạn thẳng AI bằng với độ dài của đoạn thẳng IB.
Hoặc, mặt phẳng (P) được cho trước một đoạn thẳng hoặc mặt phẳng vuông góc bất kỳ của mặt phẳng. Người học dựng đoạn thẳng sao cho (P) trở thành mặt phẳng trung trực của đoạn thẳng đó, bằng cách vẽ đoạn thẳng AB song song với đoạn thẳng hoặc đường thẳng cho trước. Đồng thời, bạn không quên thỏa mãn điều kiện rằng giao điểm của đoạn thẳng và mặt phẳng cách đều hai đầu mút của đoạn thẳng.
Trong trường hợp chỉ có một đoạn thẳng AB cho trước, người học sẽ tiến hành dựng vecto MN vuông góc với đoạn thẳng AB tại trung điểm I. Tiếp đến, bạn hãy dựng tiếp mặt phẳng (P) chứa vecto MN.
Theo đó, mặt phẳng (P) sẽ trở thành mặt phẳng trung trực của đoạn thẳng AB. Bởi mặt phẳng trung trực là tập hợp tất cả các điểm cách đều hai đầu mút của đoạn thẳng AB.
Như vậy, trên đây là tất tần tật các kiến thức có liên quan về mặt phẳng trung trực. Hy vọng rằng những thông tin này sẽ giúp bạn chinh phục toán hình một cách hiệu quả.






























